Harry,
You ask, "So how a [centreline] Z-bar connecting [centres of] front and rear axles contributes to heave/pitch stiffness?"
I think we have to start with a clearer description of what these "four-wheel-modes" mean. The following is not a rigorous definition (not enough space here) but hopefully it is of some help.
~~~~~o0o~~~~~~
Firstly, think of the car's body fixed in space (as the reference frame) and the four wheelprints moving in a generally vertical direction wrt the body. Importantly, we are not concerned with the horizontal (x,y) or rotational (Wx, Wy, Wz) constraints of the wheels or their uprights, which are a function of the control arms (beams, wishbones, whatever). We are only concerned with the approximately vertical (z) motion of the wheelprints, which is the function of the spring-dampers.
To specify the positions (heights) of the four wheelprints, wrt body, we need four numbers. The most obvious choice is LFz, RFz, LRz, and RRz (ie. the wheelprint "z" positions, or perhaps "altitudes" wrt car floorplane). A conventional "spring-at-each-corner" suspension follows this obvious approach and provides a single spring to control each of these numbers.
Now, the fact is that we have four infinities of choices as to how we specify these "four degrees of freedom" (wheelprint heights). I won't go through all these choices, just the following "all-four-wheels" method.
Here we specify our four numbers thus:
1. Bounce mode, Bz = (LFz+RFz+LRz+RRz)/4. This is also called the "Heave" mode. As the equation suggests, this is the average height of all four wheels. We can picture this mode in motion as all four wheels moving up by an equal amount (or down for negative motion).
2. Pitch mode, Pz = ((LFz+RFz)/2-(LRz+RRz)/2)/2. In words, half the difference between the average front-pair and rear-pair heights. We picture this as the two front wheels moving up, and two rear wheels moving down, an equal amount.
3. Roll mode, Rz = ((LFz+LRz)/2-(RFz+RRz)/2)/2. Similar to Pitch mode, but turned 90 degrees.
4. Twist mode, Tz = ((LFz+RRz)/2-(RFz+LRz)/2)/2 (aka "Warp" mode). This time, half the difference between the average heights of diagonal pairs.
So, as an example consider a "single wheel bounce" of left-front wheel up four units (LFz = 4 inches, 4 cm, 4 whatever), and all other wheels at "zero".
1. Bz = (4+0+0+0)/4 = 1 unit.
2. Pz = ((4+0)/2-(0+0)/2)/2 =1 unit.
3. Rz = (likewise) = 1 unit.
4. Tz = (") = 1 unit.
This is saying that a single wheel bounce of LF up 4 units (with all other wheels at zero) is equal to (Bounce = all wheels up 1 unit) + (Pitch = fronts up 1, and rears down 1) + (Roll = lefts up 1, and rights down 1) + (Twist = LF and RR up 1, and RF and LR down 1).
I hope I'm not boring you, but a useful aspect of the above is that all the modes can be measured with simple linear dimensions (inches, metres), and angular measures for P, R, and T are not needed.
~~~~~o0o~~~~~
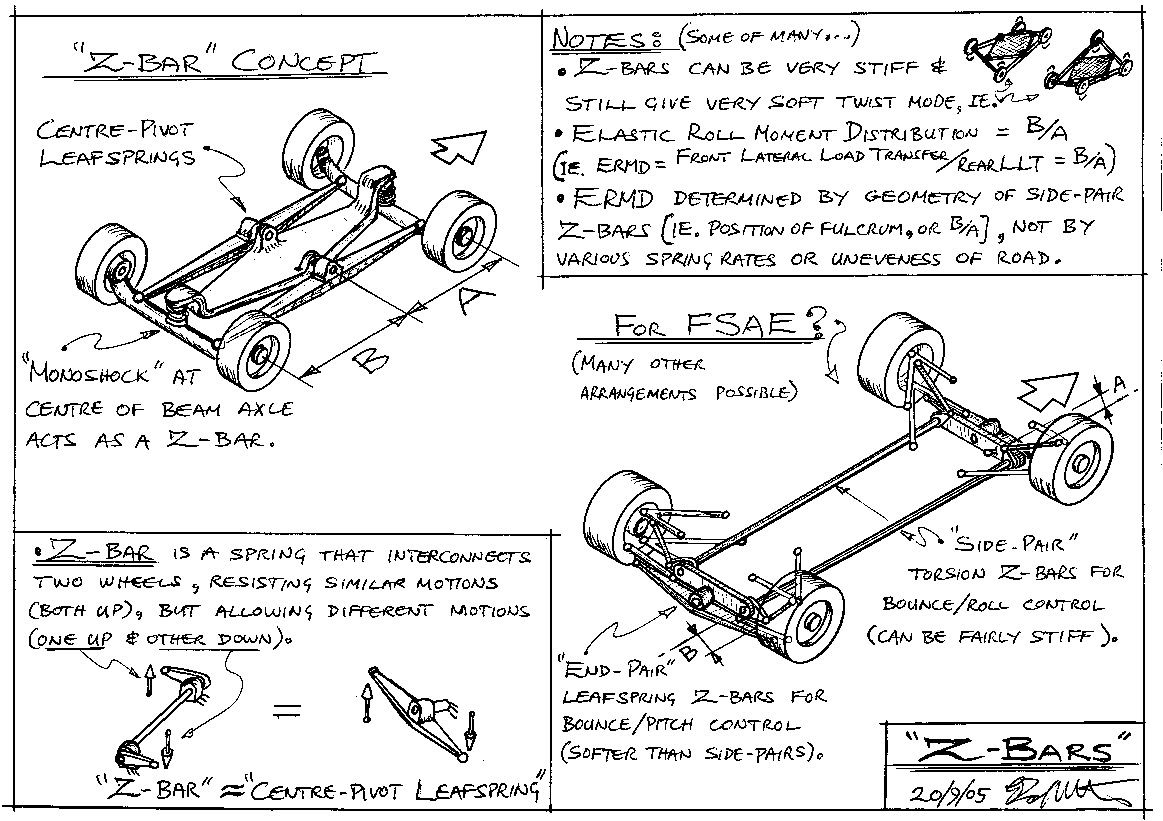
Anyway, back to your original question. I will redisplay the Z-bar sketch below because 1) it's free, 2) it is too much of a hassle to display another sketch (the sketching is easy, but then scanners, file xfers, Picassa web wanks,), and 3) hopefully it helps understanding.
Looking at the top-left of the sketch, picture only one "centre-pivot-leafspring" (= a "Z-bar") on the car centreline. Picture the ends of this leafspring as ball-jointed to the centres of the F & R beams. So now the chassis sits ONLY on the centre-pivot of this single centreline leafspring.
It should be apparent that NO Pitch, Roll, or Twist motions (as described above) can be transmitted FROM the wheelprints TO the chassis. So, the chassis responds ONLY to Bounce (=Heave) motions of the four wheelprints. So a centreline Z-bar is purely a Bounce mode spring. It does NOTHING MORE.
The above can be seen by noting that the height of the BJ at the centre of each beam provides an average of the heights of the beam's two wheelprints. The height of the centre-pivot of the leafspring then provides an average of these two averages. Thus the whole linkage (2 beams + CPL) provides an average height of all four wheelprint heights, and nothing more.
So, by INTERCONNECTING all four wheels, this linkage has SEPARATED the all-wheel Bounce mode from the other all-wheel modes (P, R, T). Similar (but a bit different) linkages connecting all wheels can give separate, or "independent", control of each of the other modes.
See SAE paper 2000-01-3572 "Balanced Suspension" , or US Patent No. 6,702,265 (lapsed), for neat ways of doing this.
~~~~~o0o~~~~~
You ask, "As I see it we have two separate issues to be resolved:
1st is axle location both longitudinal and lateral."
The Mumford Link does lateral control of a beam. My comments in earlier posts about "springing the rockers" would add axle-bounce control (but not axle-roll control). Personally, I do not think the ML is necessary for FSAE (it has too many parts for my taste), but it would work.
~~~~~o0o~~~~~
"2nd is control body movements....
The real issue to me right now is which modes you want to control, why and how."
As you say, with beam-axles it doesn't really matter how much the body moves, because the wheels always maintain the same camber. So Bounce, Pitch, and Roll can all be soft. For independent suspensions with little "camber recovery" (ie. long "virtual swing arms") it is beneficial to stiffen the Roll mode, but keep Bounce and Pitch soft (at least between limits, ie. bump stops). For sprung-aero cars the Bounce mode has to be stiff (to maintain constant ride height), but the Pitch mode can still be soft.
VERY IMPORTANTLY, in all cases there are huge advantages in having a completely soft twist mode (again, between bump stops that limit the range of twist).
It is truly astonishing that motorsports is the only sub-section of the "land vehicle" community that doesn't realise this! Even more incredible is that many of the people involved have been made aware of this, yet couldn't be bothered even thinking about it. Truly brain-dead!!! (Or just as likely, they have no need, or desire, to win!)
~~~~~o0o~~~~~
"Actually the only movement I would like to limit somehow is single wheel bump. Any thoughts on this?"
Why?
The big advantage of a soft Twist mode is that it allows the car to easily drive over large single wheel bumps.
Looking again at the example at the top of this post, if a car has rigid Bounce, Pitch, and Roll modes, and a completely soft Twist mode, then it can drive, even very slowly, over a 4" high single wheel bump with the car's CG only moving up 1", and the body only pitching 1" and rolling 1" (as defined earlier). (Picture top-left of Z-bar sketch with stiff leafs and coils, then look at top-right for the effect of a soft Twist mode.)
Most importantly, the soft Twist mode means no changes to the vertical wheel loads over bumps (not considering inertia). That is why almost everyone else bar the motorpsorts community uses it. (See Appendix of above-referenced SAE paper for examples.)
Z

|
|



 Reply With Quote
Reply With Quote